Coursera《Fundamentals of Digital Image and Video Processing》(Quiz of Week2)
Signals and Systems
本博客为Coursera上的课程《Fundamentals of Digital Image and Video Processing》第二周的测验。
目录
Coursera课程地址
第一题
1.After applying spatial filtering to an image, you find that the output image looks more blurry than the original image, i.e., some details like sharp edges are lost. Based on this description, the filter applied is most likely to be which of the following types?
A. A high-pass filter
B. A low-pass filter
C. A band-pass filter
D. A band-stop filter
答案:B
第二题
2.Which one of the following impulse responses acts a high-pass filter?
A. 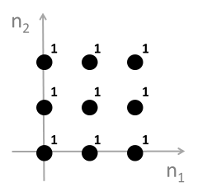
B. 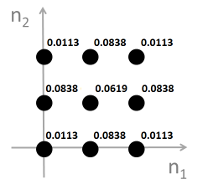
C. 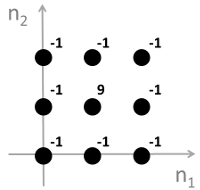
D. 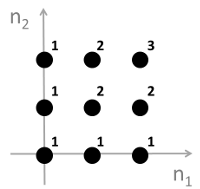
答案:C
第三题
3.What is the linear convolution of s1(n1,n2) and s2(n1,n2)?
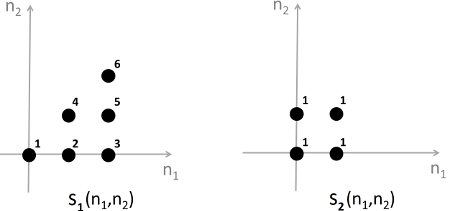
A. 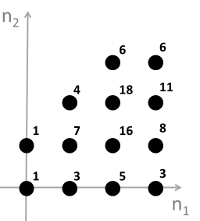
B. 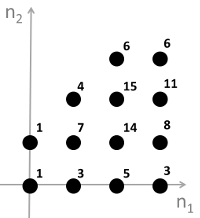
C. 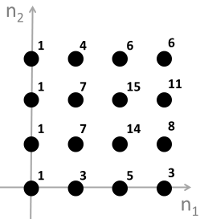
D. None of the above.
答案:B
第四题
4.A linear shift-invariant system is fully characterizable by its impulse response.
A. true
B. false
答案:A
第五题
5.Check all the statements that apply to any linear shift-invariant system T:
A. If the output to x(n1,n2)=δ(n1,n2) is known, it is possible to find the output to any other input.
B. The output to x(n1,n2)=ej(ω1n1+ω2n2) is always proportional to the input, i.e., y(n1,n2)=Cx(n1,n2) where C is a complex constant.
C. It is possible that the zero input (i.e., x(n1,n2)=0) results in a non-zero output (i.e., y(n1,n2)≠0).
D. If y(n1,n2)=0 then x(n1,n2)=0.
答案:B
第六题
6.The regions of support of two images $x(n_1,n_2)$ and $y(n_1,n_2)$ are given respectively by $S_x={(n_1,n_2)|0≤n_1≤P_1−1,0≤n_2≤P_2−1)}$ and $S_y={(n_1,n_2)|0≤n_1≤Q_1−1,0≤n_2≤Q_2−1)}$. Which of the following statements is true regarding the linear convolution of $x(n_1,n_2)$ and $y(n_1,n_2)$, i.e., $z(n_1,n_2)=x(n_1,n_2)⋆⋆y(n_1,n_2)$.
A. $z(n_1,n_2)$ is always non-zero over $Sz={(n_1,n_2)|0≤n_1≤P_1+Q_1−1,0≤n_2≤P_2+Q_2−1)}$.
B. $z(n_1,n_2)$ is always non-zero over $Sz={(n_1,n_2)|0≤n_1≤P_1+Q_1−2,0≤n_2≤P_2+Q_2−2)}$.
C. $z(n_1,n_2)$ is always zero outside $Sz={(n_1,n_2)|0≤n_1≤P_1+Q_1−1,0≤n_2≤P_2+Q_2−1)}$
D. $z(n_1,n_2)$ is always zero outside $Sz={(n_1,n_2)|0≤n_1≤P_1+Q_1−2,0≤n_2≤P_2+Q_2−2)}$.
答案:D
第七题
7.In this problem you will implement spatial-domain low-pass filtering using MATLAB, and evaluate the difference between the filtered image and the original image using two quantitative metrics called Mean Squared Error (MSE) and Peak Signal-to-Noise Ratio (PSNR). Given two N1×N2 images x(n1,n2) and y(n1,n2), the MSE is computed as $MSE=\frac{1}{N_1+N_2}$ $\sum_{n_1=1}^{N_1}\sum_{n_2=1^{N_2}}{[x(n_1,n_2)-y(n_1,n_2)]^2}$.
The PSNR is defined as $PSNR=10\lg(\frac{MAX_I^2}{MSE})$, where $MAX_I$ is the maximum possible pixel value of the images. For the 8-bit gray-scale images considered in this problem, $MAX_I$=255.
- Download the original image from here. The original image is a 256×256 8-bit gray-scale image.
- Convert the original image from type ‘uint8’ (8-bit integer) to ‘double’ (real number).
- Create a 3×3 low-pass filter with all coefficients equal to 1/9, i.e., create a 3×3 MATLAB array with all elements equal to 1/9.
- Low-pass filter the original image (converted to type ‘double’) with the filter created in step (3). This can be done using the built-in MATLAB function “imfilter”. The function “imfilter” takes three arguments and returns one output. The first argument is the original image (converted to type ‘double’); the second argument is the low-pass filter created in step (3); and the third argument is a string specifying the boundary filtering option. For this problem, use ‘replicate’ (including the single quotes) for the third argument. The output of the function “imfilter” is the filtered image.
- Compute and record the PSNR value between the original image (converted to type ‘double’) and the filtered image by using the formulae given above.
Enter the PSNR value (up to two decimal points).
答案:29.30
code:
clear;
img = imread("lena.gif");
imgd = double(img);
filter = ones(3,3)*1/9;
optimg = imfilter(imgd,filter,"replicate");
psnr1 = psnr(imgd,optimg,255);
printf("psnr1=%.2f\n",psnr1);
第八题
8.Repeat steps (3) through (5) using a 5×5 low-pass filter with all coefficients equal to 1/25. Enter the PSNR values you have obtained from your experiments (The PSNR corresponding to 3×3 filter first, followed by the PSNR corresponding to 5×5 filter). Make sure you order the answers correctly and separate them by a space. Enter the numbers to 2 decimal points.
Enter the PSNR value (up to two decimal points).
答案:25.73
code:
clear;
img = imread("lena.gif");
imgd = double(img);
filter = ones(5,5)*1/25;
optimg = imfilter(imgd,filter,"replicate");
psnr2 = psnr(imgd,optimg,255);
printf("psnr2=%.2f\n",psnr2);